№ 17.51 Геометрія = № 36.51 Математика
Бічна сторона рівнобедреного трикутника на 5 см менша від основи. Відрізки, на які бісектриса кута при основі ділить висоту, проведену до основи, відносяться як 5 : 3. Знайдіть периметр трикутника.
Розв'язок:
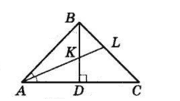
У $ΔABC\ AB = BC,$
$ AB = AC = 5$ см.
$BD ⊥ AC$ — висота, $AL$ — бісектриса кута $A.$
У $ΔABD\ BD ⊥ AD,$
$AD = \frac{1}{2}AC$ (висота є медіаною).
Оскільки $AB > AD,$ то $BK > KD, $
тоді $BK : KD = 5 : 3.$
Нехай $AC = x$ см,
тоді $AB = (x − 5)$ см,
$AD = 0{,}5x$ см.
За властивістю бісектриси:
$AB : AD = BK : KD,$
$\frac{x\ -\ 5}{0,5x}\ =\ \frac{5}{3};$
$3x – 15 = 2{,}5x;$
$0{,}5x = 15;$
$x = 30.$
Отже, $AC = 30$ см,
$AB = 30 − 5 = 25$ (см).
$P_{ΔABC} = AC + 2AB =$
$= 30 + 2 ⋅ 25 = 80$ (см).
Відповідь:
$80$ см.
