№ 17.50 Геометрія = № 36.50 Математика
Відношення бічної сторони до основи рівнобедреного трикутника дорівнює 5 : 8, а різниця відрізків, на які бісектриса кута при основі ділить висоту, проведену до основи, дорівнює 3 см. Знайдіть периметр трикутника.
Розв'язок:
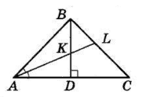
У $ΔABC AB = BC,$
$ AB : AC = 5 : 8; $
$BD ⊥ AC$ — висота, $AL$ — бісектриса.
Висота $BD,$ проведена до основи, є медіаною.
$AD = DC.$
Тоді $ AB∶ AD = 54.$
За властивістю бісектриси трикутника $\frac{AB}{AD}=\frac{BK}{KD}.$
Оскільки $AB > AD,$
то і $BK > KD.$
Нехай $KD = x$ см,
тоді $BK = (x + 3)$ см.
$\frac{5}{4}\ =\ \frac{x\ +\ 3}{x};$
$5x = 4x + 12;$
$x = 12.$
$KD = 12$ см,
$BK = 12 + 3 = 15$ (см),
$BD = BK + KD =$
$= 15 + 12 = 27$ см.
У $ΔABD\ AB^2 = $
$= BD^2 + AD^2.$
$AB = 5y, AD = 4y.$
$(5y)^2 = 27^2 + (4y)^2;$
$25y^2 = 729 + 16y^2;$
$9y^2 = 729;$
$y^2 = 81;$
$y = 9.$
$AB = 5 · 9 = 45$ (см);
$AD = 4 · 9 = 36$ (см);
$AC = 2 · AD =$
$= 2 · 36 = 72$ (см).
$P_{ΔABC} = 45 + 45 + 72 =$
$= 162$ (см).
Відповідь:
$162$ см.
