№ 17.49 Геометрія = № 36.49 Математика
Рівнобічну трапецію з основами a і b описано навколо кола. Доведіть, що її висота дорівнює √ab.
Розв'язок:
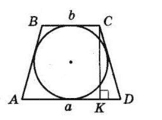
$ABCD$ — трапеція, $AD || BC, AB = CD, AD = a, BC = b.$
$CK ⊥ AD$ — висота трапеції.
Оскільки в трапецію вписано коло, то $AB + CD = AD + BC,$
тоді $2CD = a + b,$
$CD\ =\ \frac{a\ +\ b}{2}.$
$KD\ =\ \frac{AD\ -\ BC}{2}\ =\ \frac{a\ -\ b}{2}.$
$CK\ =\sqrt{CD^2 - KD^2} =$
$= \sqrt{(\frac{a+b}{2})^2 - (\frac{a-b}{2})^2} =$
$= \sqrt{\frac{a^2 + 2ab + b^2 - a^2 + 2ab - b^2}{2}} =$
$= \sqrt{\frac{4ab}{4}} = \sqrt{ab}.$
