№ 17.48 Геометрія = № 36.48 Математика
Діагоналі трапеції взаємно перпендикулярні і дорівнюють 6 см і 8 см. Знайдіть середню лінію трапеції.
Розв'язок:
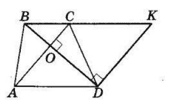
$ABCD$ — трапеція $(AD || BC), BD ⊥ AC,$
$ BD = 8$ см, $AC = 6$ см.
Продовжимо $BC$ і проведемо $DK ⊥ AC.$
Оскільки $ACKD$ — паралелограм, то $DK = AC = 6$ см.
$BD ⊥ DK,$ оскільки
$BD ⊥ AC$, а $AC || DK.$
$ΔBDK$ — прямокутний.
$BK^2 = BD^2 + DK^2.$
$BK = \sqrt{BD^2 + DK^2} =$
$= \sqrt{8^2 + 6^2} = \sqrt{64\ +\ 36} = $
$= \sqrt{100} = 10$ (см).
$BK = BC + AD,$ тоді середня лінія дорівнює $BK,$ тобто $5$ см.
Відповідь:
$5$ см.
