№ 17.47 Геометрія = № 36.47 Математика
У прямокутному △ точка дотику вписаного кола ділить катет на відрізки 2 см і 10 см. Знайдіть периметр трикутника.
Розв'язок:
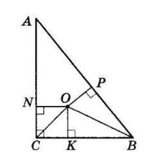
$ΔABC$ — прямокутний, $∠C = 90°.$
Центр вписаного кола $O$ — точка перетину бісектрис кутів трикутника,
$OK ⊥ BC$ — радіус вписаного кола, проведений у точку дотику.
$CK = 2$ см, $BK = 10$ см.
$OK = ON = OP.$
$ΔNOC = ΔKOC$ за гіпотенузою і гострим кутом.
Тоді $CN = CK = 2$ см.
Аналогічно $PB = BK = 10$ см,
$AP = AN = x$ см,
$AC = (x + 2)$ см,
$AB = (x + 10)$ см.
За теоремою Піфагора:
$AB^2 = AC^2 + BC^2;$
$(x + 10)^2 =$
$= (x + 2)^2 + (10 + 2)^2;$
$x^2 + 20x + 100 =$
$= x^2 + 4x + 4 + 144;$
$20x − 4x = 148 − 100;$
$16x = 48; $
$x = 3.$
$AP = AN = 3$ см;
$AC = 3 + 2 = 5$ (см);
$AB = 3 + 10 = 13$ (см).
$P_{ΔABC} = AC + BC + AB =$
$= 5 + 12 + 13 = 30$ (см).
Відповідь:
$30$ см.
