№ 17.41 Геометрія = № 36.41 Математика
Радіус кола, описаного навколо тупокутного рівнобедреного трикутника, дорівнює 37 см, а його основа – 70 см. Знайдіть бічну сторону трикутника.
Розв'язок:
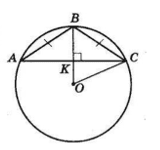
$O$ — центр кола, описаного навколо трикутника $ABC,$
$∠B$ — тупий, тому центр O знаходиться поза трикутником.
$OB = OC = 37$ см, $AC = 70$ см.
$OB ⊥ AC, AK = KC.$
У $ΔOKC\ OK = $
$= \sqrt{OC^2 - KC^2} =$
$= \sqrt{37^2 - 35^2} =$
$= \sqrt{(37\ -\ 35)(37\ +\ 35)} = $
$= 2 · 72 = \sqrt{144} = 12$ (см).
$BK = OB − OK =$
$= 37 − 12 = 25$ (см).
У $ΔBKC\ BC =$
$=\sqrt{BK^2 + KC^2} =$
$= \sqrt{25^2 + 35^2}=$
$= \sqrt{625\ +\ 1225} = \sqrt{1850} = $
$= 5\sqrt{74}$ (см).
Відповідь:
$5\sqrt{74}$ см.
