№ 17.42 Геометрія = № 36.42 Математика
Висота рівнобедреного гострокутного трикутника, проведена до основи, дорівнює 18 см, а радіус кола, описаного навколо нього, – 13 см. Знайдіть бічну сторону трикутника.
Розв'язок:
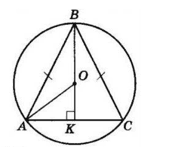
$O$ — центр кола, описаного навколо трикутника $ABC,$
$∠B$ — гострий, тому точка O лежить на висоті BK, проведеної до основи трикутника.
$BK = 18$ см, $AO = OB = 13$ см.
У $ΔAOK (∠K = 90°)$
$ AK^2 = AO^2 − OK^2.$
$OK = BK − BO =$
$= 18 − 13 = 5$ см.
Тоді:
$AK^2 = 13^2 − 5^2 =$
$= 169 − 25 = 144.$
У $ΔABK (∠K = 90°)$
$AB = \sqrt{AK^2 + BK^2} = $
$= \sqrt{144 + 18^2} = \sqrt{468} =$
$ = \sqrt{36·13} = 6\sqrt{13}$ (см).
Відповідь:
$6\sqrt{13}$ см.
