№ 17.40 Геометрія = № 36.40 Математика
Знайдіть сторони паралелограма, діагоналі якого дорівнюють 8 см і 10 см, і одна з них перпендикулярна до сторони.
Розв'язок:
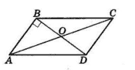
$ABCD$ — паралелограм,
$BD ⊥ AB.$
$BD = 8$ см, $AC = 10$ см.
$AO\ =\ CO\ =\ \frac{1}{2}AC\ =$
$= \ \frac{1}{2}\ · 10 = 5$ (см).
$BO\ =\ DO\ =\ \frac{1}{2}BD\ =$
$= \ \frac{1}{2}\ · 8 = 4$ (см).
У $ΔABO\ AB =$
$= \sqrt{AO^2 - BO^2} = $
$= \sqrt{5^2 - 4^2} = \sqrt{25\ -\ 16} =$
$= \sqrt9 = 3$ (см).
У $ΔABD\ AD = $
$= \sqrt{AB^2 - BD^2} =$
$= \sqrt{3^2 + 8^2} =\sqrt{9\ +\ 64} =$
$= \sqrt{73}$ (см).
Відповідь:
$3 см, \sqrt{73}$ см.
