№ 17.39 Геометрія = № 36.39 Математика
Висота BK рівнобедреного трикутника ABC (AB = AC) ділить сторону AC на відрізки AK = 24 см і KC = 1 см. Знайдіть основу трикутника.
Розв'язок:
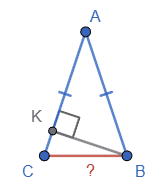
У $ΔABC\ AB = AC, BK ⊥ CA,$
$ AK = 24$ см, $KC = 1$ см.
У $ΔABC\ AC = AB =$
$= AK + KC = 24 + 1 = 25$ (см).
$BK^2 = AB^2 − AK^2 =$
$= 25^2 − 24^2 =$
$= (25 − 24)(25 + 24) =$
$= 1 · 49 = 49.$
У $ΔBKC\ CB =$
$= \sqrt{BK^2 + KC^2} =$
$= \sqrt{49\ +\ 1} =\sqrt{50} =$
$= \sqrt{25 · 2} = 5\sqrt2$ (см).
Відповідь:
$5\sqrt2$ см.
