№ 17.38 Геометрія = № 36.38 Математика
У рівнобедреному △ висота, проведена до бічної сторони, дорівнює 5 см і поділяє її на два відрізки, так що прилеглий до вершини рівнобедреного трикутника відрізок дорівнює 12 см. Знайдіть основу трикутника.
Розв'язок:
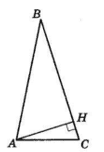
У $ΔABC\ AB = BC,$
$ AH ⊥ BC, AH = 5$ см,
$BH = 12$ см.
У $ΔAHB\ AB = $
$= \sqrt{AH^2 + BH^2} =$
$= \sqrt{5^2 + 12^2} = \sqrt{25\ +\ 144} =$
$= \sqrt{169} = 13$ (см).
$BC = AB = 13$ см,
$CH = BC − HB =$
$= 13 − 12 = 1$ (см).
У $ΔAHC:$
$AC = \sqrt{AH^2 + HC^2} = $
$= \sqrt{5^2 + 1^2} = \sqrt{25\ +\ 1} = $
$= \sqrt{26}$ (см).
Відповідь:
$\sqrt{26}$ см.
