№ 17.37 Геометрія = № 36.37 Математика
BK – висота трикутника ABC, у якого ∠C – тупий. AB = 20 см, BC = 13 см, CK = 5 см. Знайдіть AC.
Розв'язок:
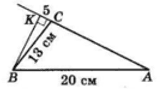
У $ΔBKC:$
$BK = \sqrt{BC^2 - KC^2} =$
$= \sqrt{13^2 - 5^2} = \sqrt{169\ -\ 25} = $
$= \sqrt{144} = 12$ (см).
У $ΔABK:$
$AK = \sqrt{AB^2 - BK^2} =$
$= \sqrt{20^2 - 12^2} = $
$= \sqrt{(20\ -\ 12)(20\ +\ 12)} = $
$= \sqrt{8 · 32} = \sqrt{8 · 4 · 8} = $
$= 8 · 2 = 16$ (см).
$AC = AK − KC =$
$= 16 − 5 = 11$ (см).
Відповідь:
11 см.
