№ 17.34 Геометрія = № 36.34 Математика
Один з катетів прямокутного трикутника дорівнює 6 см, а другий на 2 см менший від гіпотенузи. Знайдіть периметр трикутника.
Розв'язок:
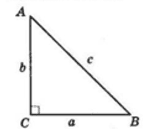
$AC = 6$ см.
Нехай $AB = x$ см, тоді $BC = (x − 2)$ см.
За теоремою Піфагора $AB^2 = AC^2 + BC^2.$
$x^2 = (x − 2)^2 + 6^2;$
$x^2 = x^2 − 4x + 4 + 36;$
$4x = 40, $
$x = 10.$
$AB = 10$ см,
$BC = 10 − 2 = 8$ (см).
$P_{ΔABC} = 6 + 10 + 8 = 24$ (см).
Відповідь:
24 см.
