Завдання № 17.32

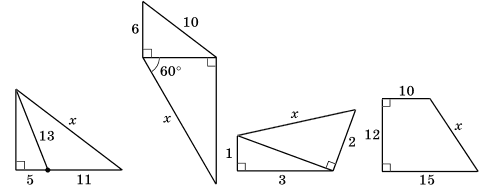
№ 17.32 Геометрія = № 36.32 Математика

Знайдіть довжину невідомого відрізка x на малюнках.

1. $ΔACD:$

$AC = \sqrt{AD^2 - CD^2} = $

$= \sqrt{13^2 - 5^2} = \sqrt{169\ -\ 25} = $

$= \sqrt{144} = 12;$

$BC = CD + BD = 5 + 11 = 16.$

$x = \sqrt{AC^2+ BC^2}= $

$=\sqrt{12^2 + 16^2} =$

$= \sqrt{144\ +\ 256} = \sqrt{400} =$

$= 20.$

2. $ΔABC:$

$BC = \sqrt{AB^2 - AC^2} = $

$=\sqrt{10^2 - 6^2} = \sqrt{100\ -\ 36} =$

$= \sqrt{64} = 8.$

$ΔBCD: ∠D = $

$= 90° − ∠BCD = $

$= 90° − 60° = 30°. $

$x = 2BC = 2 · 8 = 16.$

3. $ΔABC: $

$AB^2 = \sqrt{AC^2 + BC^2} = $

$= \sqrt{1^2 + 3^2} = 1 + 9 = 10.$

$ΔABD:$

$x = \sqrt{AB^2 + BD^2} = $

$= \sqrt{10 + 2^2} = \sqrt{14}.$

4. Проведемо $CE ⊥ AD, ABCE$ – прямокутник $(BC || AE, AB || CE, $

$∠A = 90°).$

$CE = AB = 12,$

$ AE = BC = 10.$

$DE = AD − AE =$

$= 15 − 10 = 5.$

$ΔCED:$

$x = \sqrt{CE^2 + ED^2} = $

$= \sqrt{12^2 + 5^2} = \sqrt{144\ +\ 25} = $

$= \sqrt{169} = 13.$

1. $20;$

2. $16;$

3. $\sqrt{14};$

4. $13.$