№ 17.15 Геометрія = № 36.15 Математика
Діагоналі ромба дорівнюють 24 см і 70 см. Знайдіть сторону ромба.
Розв'язок:
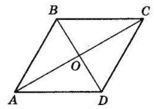
У ромбі $ABCD, AC = 70$ см,
$BD = 24$ см. Діагоналі ромба перпендикулярні і точкою перетину O діляться навпіл.
У $ΔAOB (∠O = 90°)$
$AO\ =\ \frac{1}{2}AC\ =\ \frac{1}{2}\ · 70 =$
$= 35$ (см),
$BO\ =\ \frac{1}{2}BD\ =\ \frac{1}{2}\ · 24 =$
$= 12$ (см).
$AB = \sqrt{AO^2 + BO^2} =$
$= \sqrt{35^2 + 12^2} = $
$= \sqrt{1225\ +\ 144} =$
$= \sqrt{1369} = 37$ (см).
Відповідь:
$37$ см.
