№ 17.14 Геометрія = № 36.14 Математика
Основа рівнобедреного трикутника дорівнює 16 см, а висота, проведена до основи, – 15 см. Знайдіть бічну сторону трикутника.
Розв'язок:
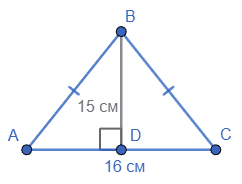
У $ΔABC, AB = BC,$
$ AC = 16$ см,
$BD ⊥ AC, BD = 15$ см.
Висота $BD$ у прямокутному трикутнику є медіаною:
$AD\ =\ DC\ =\ \frac{1}{2}AC\ =$
$= \ \frac{1}{2}\ · 16 = 8$ (см).
З $ΔABC:$
$AB^2 = AD^2 + BD^2;$
$AB = \sqrt{AD^2 + BD^2} =$
$ \sqrt{8^2 + 15^2} = \sqrt{64\ +\ 225} =$
$= \sqrt{289} = 17$ (см).
Відповідь:
$17$ см.
