ЗПЗ §§ 11–16 Геометрія = ЗПЗ §§ 23–28 Математика
Знайдіть висоту рівнобічної трапеції, основи якої дорівнюють 10 см і 6 см, а діагональ перпендикулярна до бічної сторони.
Розв'язок:
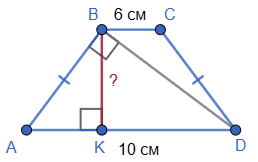
1. Нехай BK — висота рівнобічної трапеції ABCD, основи AD = 10 см; BC = 6 см.
2. AK = $\frac{AD – BC}{2}\ = \frac{10 – 6}{2} = $
$= \frac{4}{2}$ = 2 (см).
3. Тоді KD = 10 – 2 = 8 (см).
4. Оскільки ∠ABD = 90° (за умовою), то BK — висота прямокутного трикутника, яка проведена до гіпотенузи.
За властивістю висоти маємо:
BK2 = AK · KD;
BK2 = 2 · 8 = 16;
Тому BK = 4 см.
Відповідь:
4 см.
