Завдання № 10

ЗПЗ §§ 11–16 Геометрія =  ЗПЗ §§ 23–28 Математика

У двох рівнобедрених трикутниках кути при вершині між собою рівні. Периметр одного з трикутників дорівнює 56 см. Знайдіть його сторони, якщо дві сторони другого трикутника відносяться як 2 : 3.    

Розв'язок:

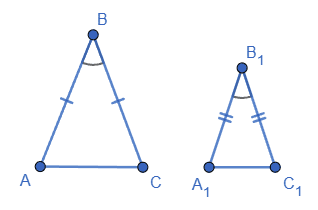
1. Нехай у ∆ABC : AB = BC, а у ∆A₁B₁C₁ : A₁B₁ = B₁C₁, крім того ∠B = ∠B₁.
Тоді ∆ABC ~ ∆A₁B₁C₁ (за наслідком з ознаки подібності трикутників за двома сторонами і кутом між ними).

2. P_∆ABC = 56 см.
Сторони трикутника A₁B₁C₁ відносяться як 2 : 3.
Оскільки ∆ABC ~ ∆A₁B₁C₁, то й сторони трикутника ABC відносяться, як 2 : 3.

3. Необхідно розглянути два випадки.

І випадок.

AB : AC = 2 : 3.

Тоді позначимо AB = BC = 2x (см), AC = 3x (см).

Маємо 2x + 2x + 3x = 56;

7x = 56;

x = 8 (см).

Тоді AB = BC = 2 · 8 = 16 (см),

AC = 3 · 8 = 24 (см).

ІІ випадок.

AC : BC = 2 : 3.

Тоді позначимо AC = 2x (см), AB = BC = 3x (см).

Маємо 2x + 3x + 3x = 56;

8x = 56;

x = 7 (см).

Тоді AC = 2 · 7 = 14 (см)

AB = BC = 3 · 7 = 21 (см).

Відповідь: 

16 см; 16 см; 24 см або 14 см; 21 см; 21 см.