Завдання № 39

ВПР 2 №39 Геометрія =  ВПТ 6 №39 Математика

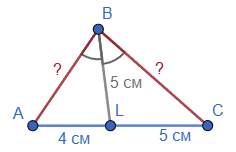
У трикутнику ABC з вершини B проведено бісектрису BL. Відомо, що BL = 5 см, AL = 4 см, LC = 5 см. Знайдіть AB і BC.    

Розв'язок:

BL² = AB ⋅ BC – AL ⋅ CL.
За властивістю бісектриси кута трикутника 

$\frac{AB}{BC}=\frac{AL}{LC}=\frac{4}{5}.$

Нехай AB = 4x, BC = 5x.
5² = 4x ⋅ 5x = 4 ⋅ 5;

25 = 20x² – 20;

45 = 20x².

$x^2\ =\ \frac{45}{20};$

$x^2\ =\ \frac{9}{4};$

$x =\ \frac{3}{2};\ x\ =\ 1{,}5.$

AB = 4 ⋅ 1,5 = 6 (см),

BC = 5 ⋅ 1,5 = 7,5 (см).

Відповідь:

6 см, 7,5 см.