ВПР 2 №37 Геометрія = ВПТ 6 №37 Математика
Продовження медіани AM рівнобедреного трикутника ABC (AB = AC) перетинає коло, описане навколо трикутника, у точці P. AM = 6 см, BC = 8 см. Знайдіть AP.
Розв'язок:
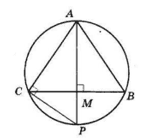
У ΔACP, ∠C = 90° як вписаний кут, що спирається на діаметр.
У ΔABC (AB = AC) AM — медіана, а значить, і висота.
Отже, AM ⊥ CB.
З ΔACP, за властивістю висоти, опущеної з вершини прямого кута, CM2 = AM ⋅ MP.
MP = CM2 ∶ AM = 42 ∶ 6 = 16 ∶ 6 = 2$\frac{2}{3}$см.
AP = AM + MP = 6 + $2\frac{2}{3}=8\frac{2}{3}$ (см).
Відповідь:
$8\frac{2}{3}$ см.
