ВПР 2 №32 Геометрія = ВПТ 6 №32 Математика
Точка D належить стороні AB трикутника ABC. Порівняйте кути ACD і BCD, якщо AC = 6 см, BC = 8 см, AD = 3 см, DB = 7 см.
Розв'язок:
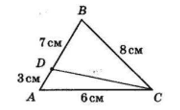
Якби відрізок CD був бісектрисою кута C, то виконувалась би рівність
$\frac{AC}{BC}=\ \frac{AD}{BD}.$
Нехай AD = x см,
тоді BD = (3 + 7 – x) = (10 – x) см.
$\frac{6}{8}\ =\ \frac{x}{10 – x};$
60 – 6x = 8x;
14x = 60;
$x\ =\ 4\frac{2}{7}.$
Отже, якщо CD — бісектриса, то AD = $4\frac{2}{7}.$
За умовою AD = 3 см, тоді ∠ACD < $\frac{1}{2}$ ∠C, отже, ∠ACD < ∠BCD.
Відповідь:
∠ACD < ∠BCD.
