Завдання № 31

ВПР 2 №31 Геометрія =  ВПТ 6 №31 Математика

Периметр прямокутника 60 см. Бісектриса, що виходить з вершини кута прямокутника, ділить його діагональ на відрізки, що відносяться як 7 : 8.  Знайдіть сторони прямокутника.

Розв'язок:

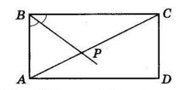
ABCD — прямокутник. 
P_ABCD = 60 см,
тоді AB + BC = $\frac{1}{2}$P_ABCD =

= $\frac{1}{2}$ ⋅ 60 = 30 (см).
Нехай AB = x см, 
то BC = (30 − x).
AC — діагональ, BP — бісектриса кута B.
AP : PC = 7 : 8.
За властивість бісектриси $\frac{AB}{AP} = \frac{BC}{PC};$

$\frac{x}{7}=\ \frac{30\ -\ x\ }{8};$

8x = 7(30 − x);

8x = 210 − 7x;

15x = 210;

x = 14.

Отже, AB = 14 см,

BC = 30 – 14 = 16 (см).

Відповідь:

14 см, 16 см.