ВПР 2 №33 Геометрія = ВПТ 6 №33 Математика
У рівнобедреному трикутнику радіус вписаного кола в 5 разів менший від висоти, проведеної до основи. Знайдіть сторони трикутника, якщо його периметр дорівнює 90 см.
Розв'язок:
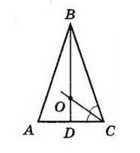
Центр кола, вписаного в трикутник — це точка перетину бісектрис.
Тоді за властивістю бісектриси
CO $\frac{CB}{CD} = \frac{BO}{OD}.$
За умовою $\frac{BO}{OD} = \frac{4}{1},$
тоді $\frac{CB}{CD} = \frac{4}{1}.$
Нехай CD = x см, тоді CB = 4x см.
PΔABCD = AB + BC + AC =
= 4x + 4x + 2x = 10x.
За умовою 10x = 90,
звідки x = 9.
Отже, DC = 9 см, AC = 2 ⋅ 9 = 18 (см).
BC = AB = 4 ⋅ 9 = 36 (см).
Відповідь:
18 см, 36 см, 36 см.
