ВПР 2 №30 Геометрія = ВПТ 6 №30 Математика
Одна зі сторін паралелограма на 9 см більша за другу. Бісектриса кута паралелограма ділить його діагональ на відрізки 4 см і 10 см. Знайдіть периметр паралелограма.
Розв'язок:
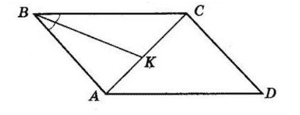
Нехай AB = x см,
тоді BC = (x + 9).
За властивістю бісектриси:
$\frac{AB}{AK}=\ \frac{BC}{KC};$
$\frac{x}{4}=\ \frac{x\ +\ 9}{10};$
10x = 4x + 36;
6x = 36;
x = 6.
Отже, AB = 6 см,
BC = 6 + 9 = 15 (см).
PABCD = 2(AB + BC) =
= 2 ⋅ (6 + 15) = 42 (см).
Відповідь:
42 см.
