Завдання № 26

ВПР 2 №26 Геометрія =  ВПТ 6 №26 Математика

Коло, вписане в ромб, точкою дотику ділить сторону ромба на відрізки 3,6 см і 6,4 см. Знайдіть діагоналі ромба. 

Розв'язок:

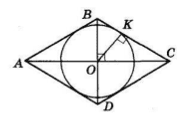
ABCD — ромб, центр вписаного кола O — точка перетину діагоналей ромба.
AC ⊥ BD,

BO = 12BD, CO = 12AC
(за властивістю діагоналей ромба).

OK ⊥ BC — радіус, проведений в точку дотику.
BK = 3,6 см, KC = 6,4 см

BC = BK + KC = 3,6 + 6,4 =

= 10 (см).

OB² = BK ⋅ BC;

OB² = 3,6 ⋅ 10 = 36;

OB = 6 см.

BD = 2OB = 2 ⋅ 6 = 12 (см)

OC² = KC ⋅ BC

OC² = 6,4 ⋅ 10 = 64,

OC = 8 см.

AC = 2 ⋅ OC = 2 ⋅ 8 = 16 (см).

Відповідь: 

8 см, 16 см.