Завдання № 25

ВПР 2 №25 Геометрія =  ВПТ 6 №25 Математика

Перпендикуляр, проведений з вершини кута прямокутника до діагоналі,  ділить її на відрізки, довжини яких відносяться як 9 : 16. Знайдіть периметр прямокутника, якщо його нижня перпендикулярна 12 см.

Розв'язок:

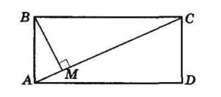
BM — висота, опущена на гіпотенузу AC з вершини прямого кута B ΔABC.
AM : MC = 9 : 16,

BM = 12 см.

Нехай AM = 9x, MC=16x

BM² = AM ⋅ MC;

12² = 9x ⋅ 16x;

144 = 144x²,

x²=1,

x=1.

Отже AM = 9 см, MC = 16 см.

AC = AM + MC = 9 + 16 =

= 25 см.

AB² = MC ⋅ AC.

AB² = 9 ⋅ 25 = 225; 

AB = 15 см.

BC² = MC ⋅ AC;

BC² = 16 ⋅ 25 = 400;

BC = 20 см.

P_ΔABC = 2(AB + BC) = 2 ⋅ (15 + 20) =

= 2 ⋅ 35 = 70 (см).

Відповідь:

70 см.