ВПР 2 №27 Геометрія = ВПТ 6 №27 Математика
У рівнобічній трапеції діагональ перпендикулярна до бічної сторони. Висота трапеції дорівнює 6 см, а середня лінія – 9 см. Знайдіть основу трапеції.
Розв'язок:
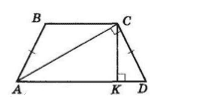
ABCD — трапеція, AD || BC, AC ⊥ BC.
CK ⊥ AD — висота, CK = 9 см.
Середня лінія трапеції дорівнює півсумі основ
$\frac{AD\ +\ BC}{2}.$
AK\ = $\frac{AD\ +\ BC}{2}.$
Тоді AK дорівнює середній лінії:
AK = 9 см.
CK2 = AK ⋅ KD,
KD =$\frac{CK_2}{AK}= \frac{36}{9} = 4$ (см).
AD = AK + KD = 9 + 4 = 13 (см).
$\frac{AD\ +\ BC}{2}=\ 9;$
13 + BC = 18;
BC = 5 (см).
Відповідь:
13 см, 5 см.
