Завдання № 24

ВПР 2 №24 Геометрія =  ВПТ 6 №24 Математика

BM – бісектриса рівнобедреного трикутника ABC (AB = BC). З точки M до BC проведено перпендикуляр MK. Знайдіть BM і периметр трикутника, якщо KC = 9 см, MK = 12 см. 

Розв'язок:

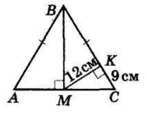
У ΔABC AB = BC.
BM — бісектриса, проведена до основи, значить, BM — висота.
MK ⊥ BC, тоді:

MK² = BK ⋅ KC;

12² = BK ⋅ 9,

звідки BK =144 : 9 = 16 (см).

BC = BK + KC = 16 + 9 = 25 (см).

BM² = BK ⋅ BC;

BM² = 16 ⋅ 25;

BM² = 400;

BM = 20 см.

MC² = KC ⋅ BC;

MC² = 9 ⋅ 25;

MC² = 225;

MC = 15 см.

AC = 2MC = 2 ⋅ 15 = 30 (см).

P_ΔABC = AC + 2BC = 30 + 2 ⋅ 25 =

= 30 + 50 = 80 (см).

Відповідь:

20 см, 80 см.