ВПР 2 №19 Геометрія = ВПТ 6 №19 Математика
У трикутник ABC вписано прямокутник KLMN, у якого KN = 16 см, LK = 10 см. Причому K ∈ AC, N ∈ AC, M ∈ BC, L ∈ AB. Знайдіть висоту трикутника, проведену з вершини B, якщо AC = 24 см.
Розв'язок:
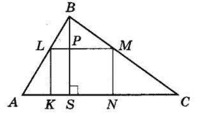
LM || KN, отже, LM || AC.
Пряма LM, паралельна стороні AC, відтинає від ΔABC подібний йому ΔLBM.
Проведемо BS ⊥ AC — висоту ΔABC, тоді BP — висота ΔLBM.
LPSK — прямокутник,
PS = LK = 10 см.
Нехай BS = x см,
тоді BP = (x − 10) см.
Отже, ΔABC ~ ΔLBM, тоді
$\frac{AC}{LM}=\ \frac{BS}{BP};$
$\frac{24}{16}\ =\ \frac{x}{x\ -\ 10};$
24x – 240 = 16x;
24x − 16x = 240;
8x = 240;
x = 30.
Отже, BS = 30 (см).
Відповідь:
30 см.
