Завдання № 18

ВПР 2 №18 Геометрія =  ВПТ 6 №18 Математика

ΔABC ∼ ΔA₁B₁C₁, точки I і I₁ – точки перетину бісектрис даних трикутників. Доведіть, що ΔAIB ∼ ΔA₁I₁B₁.  

Розв'язок:

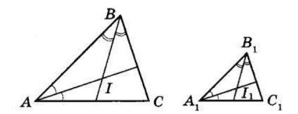
1. Оскільки ΔABC ~ ΔA₁B₁C₁, 
то ∠CAB = ∠C₁A₁B₁ і ∠CBA = ∠C₁B₁A₁.

2. ∠IAB = ∠I₁A₁B₁ (як половини рівних кутів);
∠IBA = ∠I₁B₁A₁ (аналогічно).

3. ΔAIB ~ ΔA₁I₁B₁ (за двома кутами).
Що й треба було довести.