ВПР 2 №17 Геометрія = ВПТ 6 №17 Математика
У трикутнику ABC через точку N, що належить стороні BC, проведено прямі, що перетинають сторони AB і AC відповідно в точках M і K і паралельні AC і AB. Доведіть, що MN · NK = BM · CK.
Розв'язок:
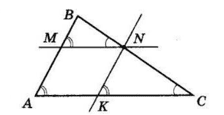
∠BNM = ∠BCA як відповідні при паралельних прямих MN і AC і січній BC.
∠BMN = ∠A як відповідні
(MN || AC, AB — січна),
∠A = ∠NKC як відповідні
(NK || AB, AC — січна),
тоді ∠BMN = ∠NKC.
ΔMBN ~ ΔKNC за двома кутами.
Звідки $\frac{MN}{KC}\ =\ \frac{BM}{NK},$
MN ⋅ NK = BM ⋅ KC.
