ВПР 2 №16 Геометрія = ВПТ 6 №16 Математика
На стороні AC трикутника ABC вибрано точку K так, що ∠BKC = ∠ABC, причому ∠BKC – тупий. Знайдіть BC, якщо AK = 16 см, CK = 9 см.
Розв'язок:
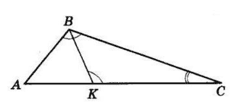
ΔABC ~ ΔBKC за двома кутами (∠C — спільний, ∠BKC = ∠ABC за умовою).
Значить, $\frac{BC}{AC}\ =\ \frac{KC}{BC};$
BC2 = AC ⋅ KC;
BC2 = (16 + 9) ⋅ 9;
BC2 = 25 ⋅ 9;
BC = 15 (см).
Відповідь:
15 см.
