ВПР 2 №12 Геометрія = ВПТ 6 №12 Математика
Діагоналі трапеції діляться точкою перетину у відношенні 2 : 3. Менша основа трапеції дорівнює 8 см. Знайдіть більшу основу трапеції.
Розв'язок:
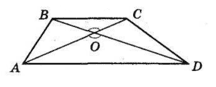
ΔBOC ~ ΔDOA за двома сторонами і кутом між ними:
∠BOC = ∠DOA як вертикальні,
$\frac{BO}{OD}= \frac{CO}{OA}\ = \frac{2}{3}$ за умовою.
Тоді $\frac{BC}{AD}= \frac{2}{3},$ звідки
AD = $ \frac{3BC}{2}= \frac{3 \cdot8}{2}=12$ (см).
Відповідь:
12 см.
