ДСР 3 Геометрія = ДСР 6 Математика
У трикутнику, сторони якого дорівнюють 8 см, 12 см і 15 см, проведено півколо, центр якого належить більшій стороні трикутника і яке дотикається до двох інших сторін. На які відрізки центр півкола ділить більшу сторону трикутника?
A. 6 см і 9 см;
Б. 8 см і 7 см;
В. 7,5 см і 7,5 см;
Г. 5 см і 10 см.
Розв'язок:
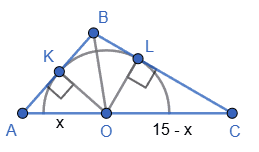
1. ∆OKB ~ ∆OLB (за катетом і гіпотенузою),
тому ∠KBO = ∠LBO.
2. BO — бісектриса ∆ABC.
3. Позначимо AO = x см, тоді OC = 15 – x см.
4. За властивістю бісектриси $\frac{AB}{AO} = \frac{BC}{OC};$
$\frac{8}{x}= \frac{12}{15 – x};$
120 – 8x = 12x;
20x = 120;
x = 6 (см).
5. Отже, AO = 6 см;
OC = 15 – 6 = 9 см.
Відповідь:
A. 6 см і 9 см.
