ДСР 3 Геометрія = ДСР 6 Математика
У ∆ABC : ∠C=90°, CK – висота трикутника, KB = 9 см, AK ∶ CK = 4 ∶ 3. Установіть відповідність між сторонами трикутника ABC(1–3) та їхніми довжинами (A–Γ).
Сторона трикутника
1. AB
2. BC
3. AC
Довжина
A. 15 см
Б. 16 см
B. 20 см
Г. 25 см
Розв'язок:
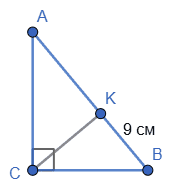
Для прямокутного трикутника з висотою з прямого кута маємо:
CK2=AK ∙ KB,
AC2=AK ∙ AB,
BC2=KB ∙ AB.
З умови AK : CK = 4 : 3 $\Rightarrow$
$\Rightarrow$ AK= $\frac{4}{3}$CK.
Тоді CK2 = AK ∙ KB = $\frac{4}{3}$CK ∙ 9 $\Rightarrow$
$\Rightarrow$ CK = 12 см,
AK = $\frac{4}{3}\cdot12=16$ см,
AB = AK + KB = 16 + 9 = 25 см.
Далі
AC2=AK ∙ AB = 16 ∙ 25 = 400 $\Rightarrow$
$\Rightarrow$ AC = 20 см,
BC2=KB ∙ AB = 9 ∙ 25 = 225 $\Rightarrow$
$\Rightarrow$ BC = 15 см.
Відповідь:
1 — Г,
2 — А,
3 — В.
