Завдання № 16.21

№ 16.21 Геометрія =  № 28.21 Математика

Знайдіть бісектрису AL трикутника ABC, якщо AC = 15 см, AB = 12 см, BC = 18 см.   

Розв'язок:

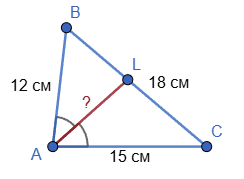
Скористаємось формулою, доведеною в задачі 1 § 17:
AL² = AB ⋅ AC – BL ⋅ CL.
Нехай CL = x см, тоді BL = (18 − x) см.
За властивістю бісектриси:

$\frac{AC}{CL}$=  $\frac{AB}{BL}$;

$\frac{15}{x}$=  $\frac{12}{18 - x}$;

15 (18 − x) = 12x.

270 − 15x = 12x;

27x = 270;

x = 10.

Отже, CL = 10 см,

BL = 18 − 10 = 8 (см).

AL² = 12 ⋅ 15 – 8 ⋅ 10 =

= 180 – 80 = 100;

AL = 10 (см).

Відповідь:

10 см.