№ 15.9 Геометрія = № 27.9 Математика
Бісектриса трикутника ділить сторону на відрізки, різниця довжин яких 1 см. Знайдіть периметр трикутника, якщо дві інші сторони дорівнюють 8 см і 6 см.
Розв'язок:
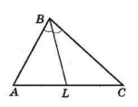
BL — бісектриса ΔABC. Відомо: AB = 8 см, BC = 6 см.
Оскільки AB > BC, то AL > LC.
Нехай LC = x см, тоді:
AL = (x + 1) см.
$\frac{AB}{AL} = \frac{BC}{LC}$;
$\frac{8}{x+1} = \frac{6}{x}$;
8x = 6x + 6;
2x = 6;
x = 3.
Отже, LC = 3 см, AL = 3 + 1 = 4 (см).
PΔABC = AB + BC + AC =
= 8 + 6 + (3 + 4) = 21 (см).
Відповідь:
21 см.
