№ 15.10 Геометрія = № 27.10 Математика
Основа рівнобедреного трикутника дорівнює 18 см, а бісектриса ділить бічну сторону на відрізки, з яких той, що суміжний з основою, дорівнює 12 см. Знайдіть периметр трикутника.
Розв'язок:
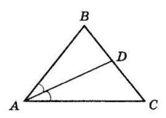
У ΔABC AB = BC, AD — бісектриса кута A.
AC = 18 см, DC = 12 см.
Нехай BD = x см,
тоді AB = (x + 12) см.
За властивістю бісектриси
$\frac{AB}{BD} = \frac{AC}{CD}$;
$\frac{x+12}{x} = \frac{18}{12}$;
12x + 144 = 18x;
18x − 12x = 144;
6x = 144,
x = 24.
Отже, BD = 24 см,
AB = BC = 24 + 12 = 36 (см).
PΔABC = 2AB + AC =
= 2 ⋅ 36 + 18 = 90 (см).
Відповідь:
90 см.
