№ 15.7 Геометрія = № 27.7 Математика
У трикутнику ABC AB = 6 см, BC = 12 см. Більший з відрізків, на які бісектриса BK ділить сторону AC, дорівнює 6 см. Знайдіть AC.
Розв'язок:
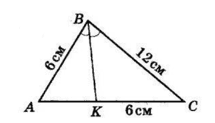
Оскільки BC > AB, то KC > AK, тоді KC = 6 см.
$\frac{AB}{AK} = \frac{BC}{KC}$;
AK =$\frac{AB ⋅ KC}{BC}$;
AK =$\frac{6 ⋅ 6}{12}$ = 3 (см).
AC = AK + KC = 3 + 6 = 9 (см).
Відповідь:
9 см.
