Завдання № 15.16

№ 15.16 Геометрія =  № 27.16 Математика

У трикутнику ABC проведено висоту CH, причому CH² = AH · BH і точка H належить стороні AB. Доведіть, що трикутник ABC – прямокутний (∠C = 90°).     

Розв'язок:

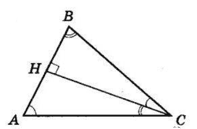
За умовою: CH² = AH ⋅ BH,
звідки $\frac{AH}{CH} = \frac{CH}{BH}$.
Тоді ΔCHB ~ ΔAHC за двома сторонами і кутом між ними (∠CHB = ∠CHA = 90°).
У подібних трикутниках відповідні кути рівні:
∠HAC = ∠HCB,
∠HCA = ∠HBC.
Але у ΔAHC (∠AHC = 90°)
∠HAC+∠HCA=90°.
Отже, ∠C = ∠HCA + ∠HBC = 90°.
Отже, ΔABC — прямокутний (∠C=90°).