№ 15.15 Геометрія = № 27.15 Математика
Чи може діагональ AC трапеції ABCD ділити навпіл і кут A, і кут C?
Розв'язок:
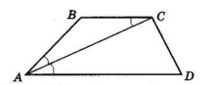
Нехай діагональ AC трапеції ABCD є бісектрисою кута A:
∠BAC=∠CAD.
∠BCA=∠CAD як внутрішні різносторонні при паралельних прямих AD і BC і січній AC.
Якщо б AC була бісектрисою і для кута C, то ∠ACD дорівнював би куту CAD, і кут A дорівнював би куту C.
Але це неможливо, оскільки протилежні кути трапеції не рівні.
Отже, бісектриса кута A не може бути бісектрисою кута C.
Відповідь:
ні.
