№ 15.14 Геометрія = № 27.14 Математика
Сторони паралелограма дорівнюють a і b (a > b). Знайдіть відрізки, на які бісектриса гострого кута ділить його більшу сторону.
Розв'язок:
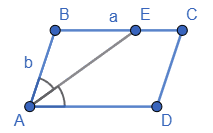
Нехай ABCD заданий паралелограм, у якого AD = BC = a, AB = CD = b. Бісектриса кута A перетинає сторону BC в точці E. Знайти CE і BE.
∠BEA = ∠EAD (як внутрішні різносторонні паралельних BC∥AD при січній AE).
Оскільки ∠BEA = ∠EAB, то ∆EAB – рівнобедрений. Отже BE = AB = b.
Тоді CE = BC – BE = a – b.
Відповідь:
b і a – b.
