Завдання № 14.22

№ 14.22 Геометрія =  № 26.22 Математика

Коло, вписане в трапецію, ділить точкою дотику одну з бічних сторін на відрізки завдовжки 2 см і 8 см, а іншу – на відрізки, один з яких дорівнює 4 см. Знайдіть периметр трапеції.      

Розв'язок:

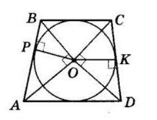
ABCD — трапеція (AD || BC), O — центр вписаного кола.
OP ⊥ AB, OK ⊥ CD — радіуси, проведені в точки дотику.
BP = 2 см, AP = 8 см, CK = 4 см.
∠OBA = $\frac{1}{2}$∠B;
∠OAB = $\frac{1}{2}$∠A;
∠OBA + ∠OAB = $\frac{1}{2}$∠B + $\frac{1}{2}$∠A = $\frac{1}{2}$ (∠B + ∠A) = $\frac{1}{2}$ ⋅ 180° = 90°. 
ΔAOB — прямокутний (∠AOB = 90°.).
ΔAOB — прямокутний (доведення див. у № 14.5).
OP² = AP ⋅ PB;
OP² = 2 ⋅ 8;
OP² = 16;
OP = 4 см.
OK = OP як радіуси.
OK² = CK ⋅ KD;
4² = 4 ⋅ KD;
KD = 16 : 4;
KD = 4 см.
AB = AP + PB = 2 + 8 = 10 (см),
CD = CK + KD = 4 + 4 = 8 (см).
Оскільки в трапецію вписано коло, то сума її основ дорівнює сумі бічних сторін.
Тоді:
P_ABCD = 2(AB + CD) =
= 2(10 + 8) = 36 (см).

Відповідь:

36 см.