Завдання № 14.21

№ 14.21 Геометрія =  № 26.21 Математика

Коло, вписане в трапецію, ділить точкою дотику бічну сторону на відрізки завдовжки 4 см і 9 см. Знайдіть висоту трапеції.    

Розв'язок:

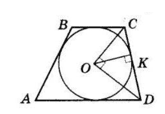
Центр вписаного в трапецію кола — це точка перетину бісектрис кутів трапеції:
∠OCK = $\frac{1}{2}$∠C;
∠ODK = $\frac{1}{2}$∠D;
∠OCK + ∠ODK=
= $\frac{1}{2}$∠C + $\frac{1}{2}$∠D = $\frac{1}{2}$ (∠C + ∠D) =
= $\frac{1}{2}$ ⋅ 180° = 90°.
Тоді ΔCOD — прямокутний, ∠COD = 90°.
OK ⊥ CD — радіус, проведений у точку дотику.
OK² = CK ⋅ KD;
OK² = 4 ⋅ 9;
OK² = 36;
OK = 6 см.
Висота трапеції дорівнює двом радіусам вписаного кола:
h = 2OK = 2 ⋅ 6 = 12 (см).

Відповідь:

12 см.