№ 13.9 Геометрія = № 25.9 Математика
На сторонах KL і KN трикутника KLN відповідно позначено точки A і B так, що
KA = $\frac{2}{3}$KL, KB = $\frac{2}{3}$KN. Доведіть, що ΔKAB ∼ ΔKLN.
Розв'язок:
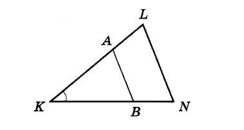
ΔKAB ~ ΔKLN за двома сторонами і кутом між ними:
∠K — спільний;
KL : AK = KL : $\frac{2}{3}$ KL = 3 : 2;
KN : KB = KN : $\frac{2}{3}$ KN = 3 : 2.
