№ 13.50 Геометрія = № 25.50 Математика
Доведіть, що бісектриси кутів прямокутника, який не є квадратом, перетинаючись, утворюють квадрат.
Розв'язок:
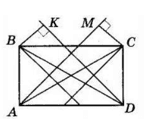
Оскільки бісектриси сусідніх кутів паралелограма перетинаються під прямим кутом, то при їх перетині утворюється прямокутник.
Проведемо з вершин B і C прямокутника ABCD перпендикуляри BK і CM на бісектриси кутів D і A відповідно.
З рівності прямокутних трикутників AMC і DKB (за гіпотенузою і гострим кутом) випливає, що MC = KB. Довжини цих відрізків — це відстані між бісектрисами протилежних кутів прямокутника ABCD, тобто довжини сторін утвореного прямокутника. Отже, сторони утвореного прямокутника рівні, тоді це квадрат.
