Завдання № 13.49

№ 13.49 Геометрія =  № 25.49 Математика

Кожна з бічних сторін рівнобедреного трикутника дорівнює a см. З точки, узятої на основі трикутника, проведено прямі, паралельні бічним сторонам. Обчисліть периметр паралелограма, який утворився.    

Розв'язок:

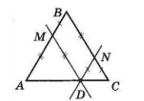
MD || DN за умовою.  
Тоді ∠AMD = ∠B як відповідні при паралельних прямих MD і BC і січній AB.  
Аналогічно, ∠DNC = ∠B як відповідні при паралельних прямих DN і AB і січній BC.  
Отже, ΔAMD = ΔDNC.  
Паралельні сторонам прямі MD і DN витинають від ΔABC трикутники AMD і DNC, подібні йому.  
Тоді ΔAMD ~ ΔDNC за кути при вершині.  
AM = MD, DN = NC.  
P_MBND = MB + BN + ND + MD =

= MB + AM + BN + NC =

= AB + BC = 2a (см).

Відповідь:

2a см.