№ 13.48 Геометрія = № 25.48 Математика
У рівнобічній трапеції ABCD (AD ∥ BC) E – середина AD, F – середина BC, K – середина AB. Доведіть, що KE = KF.
Розв'язок:
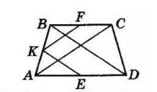
Проведемо діагоналі AC і BD трапеції ABCD.
K — середина AB, F — середина BC за умовою.
Отже, KF — середня лінія ΔABC, KF = $\frac{1}{2}$ AC.
Аналогічно, KE — середня лінія ΔABD, KE = $\frac{1}{2}$ BD.
Оскільки в рівнобічній трапеції діагоналі рівні, то KF = KE як половини рівних відрізків.
