№ 13.46 Геометрія = № 25.46 Математика
У рівнобедрений трикутник, основа якого дорівнює 6 см, а бічна сторона – 10 см, вписано коло. Знайдіть відстань між точками дотику кола до бічних сторін.
Розв'язок:
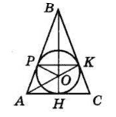
Нехай P і K — точки дотику вписаного кола з бічними сторонами AB і BC рівнобедреного ΔABC, H — точка дотику з основою.
ΔAPO = ΔAHO за катетом і гіпотенузою (AO — спільна гіпотенуза, PO = HO як радіуси).
Тоді AP = AH = $\frac{1}{2}$ AC = $\frac{1}{2}$ · 6 = 3 (см).
BP = AB − AP = 10 − 3 = 7 (см).
Оскільки PB = PK, то ΔPBK ~ ΔABC за кутом при вершині:
$\frac{PK}{AC} = \frac{BP}{AB};$
PK = $\frac{AC·BP}{AB} = \frac{6·7}{10}$= 4,2 (см).
Відповідь:
4,2 см.
