№ 13.42 Геометрія = № 25.42 Математика
У прямокутний трикутник ABC з катетами a см і b см і прямим кутом A вписано квадрат AKLM, K ∈ AB, L ∈ BC, M ∈ AC. Знайдіть сторону квадрата.
Розв'язок:
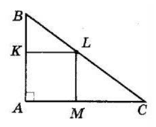
AB = a, AC = b.
Нехай AK = KL = LM = AM = x.
У ΔBKL: ∠BLK = 90° − ∠B.
У ΔABC: ∠C = 90° − ∠B.
Отже, ∠BLK = ∠C, тоді за наслідком з теореми про ознаки подібності трикутників ΔBKL ~ ΔLMC.
$\frac{BK}{KL}=\ \frac{LM}{MC};$
$\frac{a\ -\ x}{x}=\ \frac{x}{b\ -\ x};$
(a − x)(b − x) = x2;
ab − ax − bx + x2 = x2;
ab = ac + bx;
ab = (a + b)x;
$x\ =\frac{ab}{a\ +\ b}.$
Відповідь:
$\frac{ab}{a\ +\ b}$ см.
