№ 13.37 Геометрія = № 25.37 Математика
Дано два рівнобедрених трикутники. Кут при основі одного трикутника дорівнює куту при основі другого. Сторони одного з трикутників відносяться як 5 : 8, а периметр другого дорівнює 126 см. Знайдіть сторони другого трикутника. Скільки випадків слід розглянути?
Розв'язок:
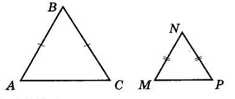
За наслідком з теореми про ознаки подібності трикутників ΔABC ~ ΔMNP.
Розглянемо два випадки.
1. MN : MP = 5 : 8,
тоді AB : AC = 5 : 8.
AB = BC = 5x, AC = 8x.
За умовою 5x + 5x + 8x = 126;
18x = 126;
x = 7.
AB = BC = 5 · 7 = 35 (см);
AC = 8 · 7 = 56 (см).
2. MN : MP = 5 : 8, тоді AC : AB = 5 : 8.
AB = BC = 8x, AC = 5x.
За умовою 8x + 8x + 5x = 126,
21x = 126,
x = 6.
AB = BC = 8 · 6 = 48 (см).
AC = 5 · 6 = 30 (см).
Відповідь:
1. 35 см, 35 см, 56 см;
2. 48 см, 48 см, 30 см.
